How Do We Tell Distance By Parallax?
Measuring distances by parallax depends on noting how the position an object seems to change when you change your point of view.
Hand out mini-stars.
Pretend that the little ball you are holding is star. Notice it is shaped like a ball—it doesn’t have points on it! Like our sun, stars are ball-shaped and they are huge—thousands of times bigger than the Earth.
We are going to see how to measure the distance to this star by looking at it from different points of view.
Hold your star out at arm’s length and look at your star against the background of the other more distant stars in the sky. Without moving your arm or head, look at your star first through one eye and then the other eye. If you need to, use your free hand to block one eye and then the other.
Does the star seem to shift position against the background stars? [Yes]
The shift in position of your star is known as parallax.
Now try holding your star closer by bending your elbow, so that the star is about half an arm’s length away. Do the same thing as before: without moving the star or your head, look at your star first through one eye and then the other eye.
Does the star’s position seem to shift less than before?
[No, the shift is more.]
So a nearby star seems to shift back and forth when we view it from different viewing points. More distant stars seem to shift less than more nearby stars.
But how can we look at a real star from different viewing points? Does anyone have any ideas?
[Accept all answers as reasonable ideas.]
The first people who tried this observed stars from different cities very far from each other, but they saw no shift at all. The stars were too far away for any parallax shift in position to be noticeable. They were able to measure the parallax shift for the Moon.
DIGITAL EFFECT: Parallax Distance
Crossfade the scene to view Earth, and a scaled up (10x) Moon with the Moon orbit on. Set date again to 2012/10/02, 13:10:00.
VISUAL 12 (still): Diagram of Measuring Moon Distance by Parallax Fade on a still graphic depicting measuring the parallax of the Moon using widely separated locations on Earth as a baseline. Point out vertices of the triangle, explaining that the base of the triangle would be two different locations on Earth.
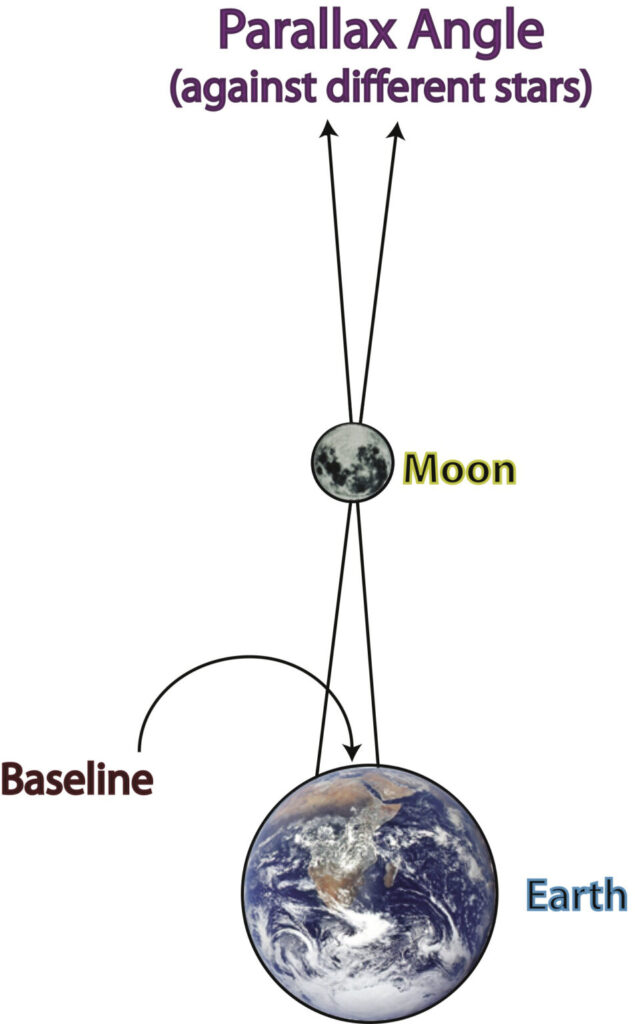
Observers were able to measure the two angles at the bottom of the triangle and then determine the height of the triangle that represented the distance to the Moon. In this way, they calculated how far away our Moon was hundreds of years before radar was invented. The base of the triangle, that represented the change in viewing point, was called the baseline.
The method called parallax, which you have just used, was the first way humankind measured distances in space. In 150 BC, the Greek astronomer Hipparachus used parallax to measure the distance to the Moon. The parallax angle he found was nearly one degree. His answer is only a percent different from the number we can measure today. Pretty good for someone 17 centuries before the invention of the telescope!
Astronomers tried to measure the parallax of the planets and the Sun, but the angle was way too small for them to measure. That meant the planets and Sun were much further away than the Moon. But how much further? It took better instruments to measure those tiny angles. Indeed, it was 16 centuries before the parallax to any other body in the solar system was finally measured.
In 1672, French astronomers just barely succeeded in measuring the parallax of Mars, and at last we had an idea how big the solar system was. The Sun was at least 140 million kilometers away! Over the next 100 years these distances were confirmed and refined to the modern value of 150 million kilometers.
But people were still left with the problem of determining the distances to the stars. Any baseline on Earth was not long enough for making a parallax measurement.
Can you guess how they did it?
[No, they didn’t have spaceships to carry them farther from the Earth.]
A breakthrough came when astronomers realized the Earth itself changes position in space as it travels around the Sun.
VISUAL 13 (still): Measuring Parallax of a Star
Fade on a still graphic depicting measuring parallax to nearby stars using Earth’s orbital diameter as a baseline.
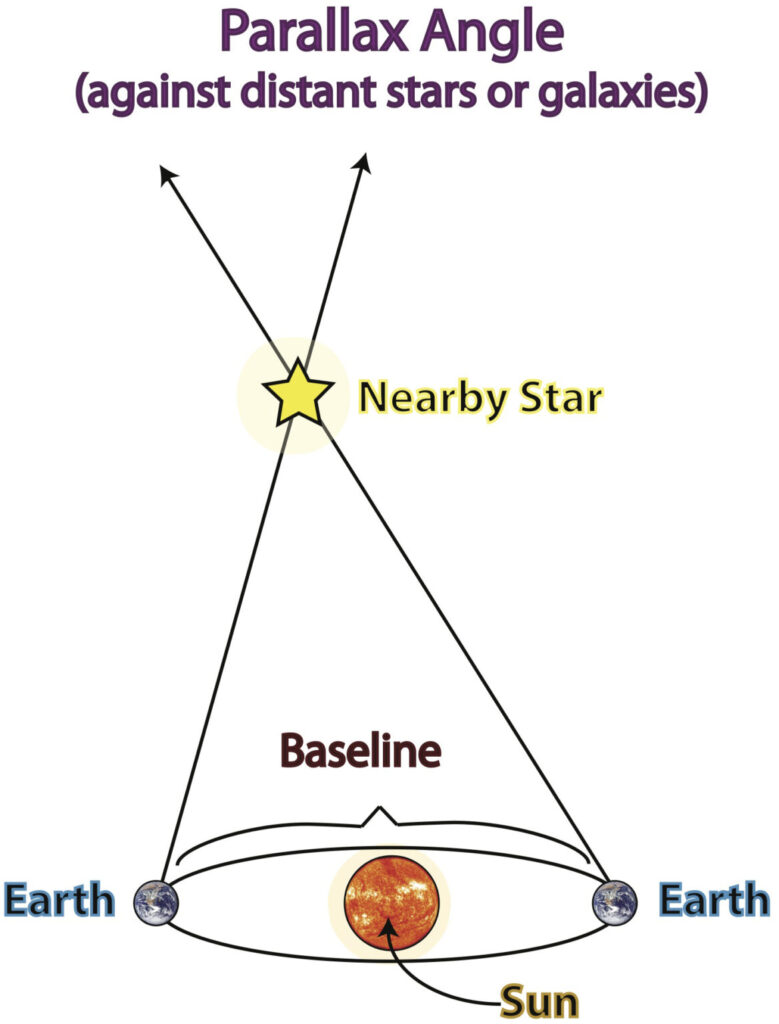
As the Earth travels around the Sun each year, we change our point of view by over 300 million kilometers! That’s the kind of baseline we need to see the parallax of a star. When astronomers take pictures of the same region of sky six months apart, some stars—the closest ones to us—change position!
To model this, hold your model star at arm’s length. Imagine that your nose is the Sun and your eyes represent the Earth at two points in its orbit, six months apart. To “take a picture” of the sky six months apart, look first through one eye and then the other. Or if you prefer using only one eye, simply move your head until your eye has moved about the distance that your eyes are apart from one another.
DIGITAL EFFECT: Earth/Star Parallax
Fade off the Moon parallax image, and fly to edge-on view of Earth’s orbit, with Sun at center, and Earth positioned at the far left. Highlight Earth’s position for easier viewing. Also scale down the Moon’s size in this step. Note: The Lawrence Hall of Science uses a default Moon size of 5x. Adjust as desired to use 2.5x or your theater’s own scale setting.
Advance time 6 months later.
The parallax of your star is amount that it seems to jump against the background stars. The greater the jump, the closer the star is to Earth. Astronomers tried to use parallax on the stars in the 15th, 16th, 17th, and 18th centuries: and they all failed. Even with the enormous baseline of the diameter of the Earth’s orbit, the parallax to the brightest (and presumably nearest) stars always came out to be 0 degrees. They were back to having to assume all the stars were infinitely far away.
Finally in 1838 Friedrich Bessel, after a year and a half of observations of one star, 61 Cygni, succeeded in measuring the parallax to a star. The parallax was less than one 10-thousandth of one degree! No wonder it was so hard to measure. Doing the same kind of calculation and graphs that you used, Bessel calculated that 61 Cygni, one of the nearest stars to us, was an incredible 25 TRILLION kilometers away. That’s 25 thousand billion kilometers!
Astronomers have found that the star which makes the biggest jump every six months is Alpha Centauri. It is “only” 10 trillion kilometers away.
Fade off the stellar parallax image and Earth’s orbitline. Also scale Earth back to default size of 1x.
Optional: Quantitative Parallax Measurement
You can do a real parallax measurement for your star.
OPTIONAL VISUAL 14 (still): Zenith Circles Fade on a graphic of concentric circles at the zenith for the optional audience activity to make a quantitative measurement of parallax. The spacing between lines should have been adjusted to be 1°.
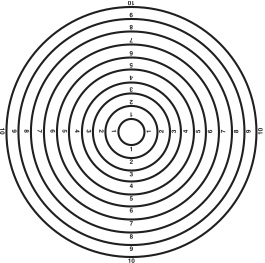
We can measure parallax angles by using these degree markings. There would be 360 degree marks in the complete circle. If your star seemed to jump all the way across the sky, from horizon to horizon, its parallax angle would be 180°. Hold your star at arm’s length, and with one eye closed, line it up so that the top of it is at the center of the bull’s eye when you look at it through one eye. Without moving your star or your head, note how many degrees the top of the star shifts when you look first through one eye and then the other. That is the parallax angle of your star. Do not use the left side or right side of the star for this measurement. The easiest method is to use the “centerline” of the star for measuring the shift. For centerline, you can use either the small stick that comes out the bottom, or the “top” point of the star. Please remember your parallax angle. To calculate how far away your star is, you need a worksheet. [Hand out a “How Far Is The Star” worksheet to each student. Increase light so students can read. If students have pencils, they can write their parallax angles down somewhere on the worksheet.] [Refer again to Visual 13, Measuring Parallax of a Star. Point to parts of the triangle as you explain.] In measuring distance by parallax, the shift in the observing position is the baseline. You used one eye and then the other to shift your observing position, so your baseline was the distance between your eyes—only a few centimeters. Remember in your model, the distance between your eyes represents a baseline that is the diameter of the Earth’s orbit. The sight lines from your eyes to the star form the sides of the triangle. Knowing the length of the baseline and the parallax angle, we know the keys to the unique triangle that is formed by the two observing positions and the star. The height of that triangle is the distance to the star. Before you can do your calculation, you need to know the baseline that is distance between your eyes. There are three drawings on the worksheet for three different baseline eye separations of 5 cm, 6 cm, and 7 cm. Please work with a partner to measure the distance between the pupils of your eyes. [Hand out tape measures or rulers.] Now that you know the baseline and the parallax angle, you can find the distance to your star. Use the diagram that is for your eye separation, the left one for eyes 5 cm apart, the middle one for eyes 6 cm apart, and the right one for eyes 7 cm apart. Then simply see what distance corresponds to the parallax angle that you measured. Your estimate should be pretty close. Check it with your partner by actually measuring the distance from your eye to your star with the tape measure (or ruler). How close were you? With real stars, there is no ruler long enough to make a check like this. We have to believe our measurements and calculations. [Collect model stars and rulers/tape measures.] Note: This entire activity can be done outside the planetarium, after the program. It works well as part of the “How Far Is It?” classroom activity.

